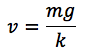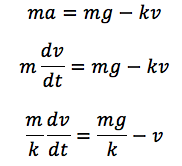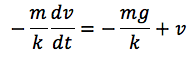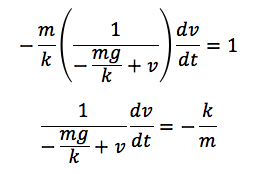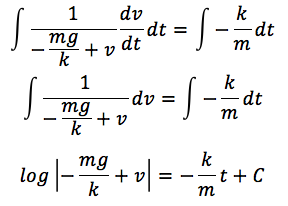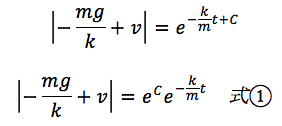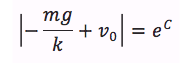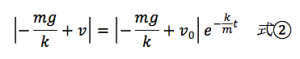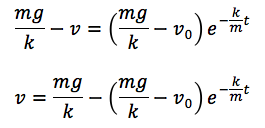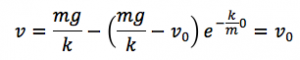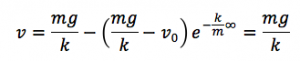雨の速度はなぜ一定になるのか?すぐわかる!微積で物理
サイエンストレーナーの桑子研です。毎日が実験。
空から降ってくる雨粒。私たちは傘をさせば、特に気にも留めませんよね。でも、少し不思議に思いませんか? 雲が浮かんでいるのは、はるか上空の数千メートル。もしそこからパチンコ玉が落ちてきたら…と考えると、ものすごい速さになって地面に激突しそうです。それなのに、雨粒が当たっても痛くないのはなぜでしょう?

実はこの謎を解く鍵こそが、物理の世界の奥深さを示しています。そして、その謎解きの冒険には、「微分積分」という、まるで魔法のような数学の道具が欠かせません。「うわ、数学の話…?」と思った方も、ご安心ください。今回は、数式の意味を一つひとつ解き明かしながら、「なるほど、物理ってこうやって世界のナゾを解くのか!」と感じてもらえるような、知的好奇心をくすぐる旅にご案内します。
なぜ物理に「微分積分」という武器が必要なのか?
高校の物理の教科書では、実は「微分積分」をあまり使わずに説明が進みます。これは、数学の授業で習う順番に配慮しているからなのですが、本来、物理現象の多くは微分積分と深く結びついています。
特に、今回テーマにする「空気抵抗」のように、「速さが変わると、受ける力も変わる」といった刻一刻と状況が変化する運動を考えるとき、微分積分は最強の武器になります。変化の「瞬間」を切り取って分析し、それをつなぎ合わせて未来を予測する。そんな魔法のような計算が、微分積分なのです。
今回は、雨粒が空から落ちてくるときの運動を例に、微分積分の威力を見ていきましょう!
世界をシンプルに!空気抵抗の正体
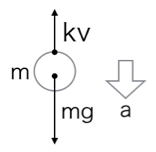
雨粒が落ちてくるとき、下向きに引っ張る「重力」と、それを邪魔する上向きの「空気抵抗」という2つの力が働いています。空気抵抗は、物体の速さが速くなるほど大きくなる、まるで意地悪なブレーキのような力です。
まずはじめに最も簡単なモデルである、速さに比例する空気抵抗kvが働く場合について今回は考えます。雨粒が上空から落下してくる様子をイメージしてみましょう。
加速度を微分すると、落下する物体に働く合力はmg−kvと表されますので、運動方程式を作ると次のようになります。
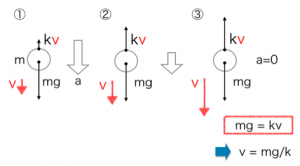
ここで入試の問題としては、終端速度を問う問題がでます。はじめは速度が小さいので、kvの値は小さくなり加速をします①。しかし速度が増えると、kvの値が大きくなり、加速度も小さくなります②。そして最終的にはkvとmgがつりあいます。
このことから終端速度は、
と表されます。ただ、一体どのようにして速度がmg/kに近づいていくのでしょうか。微積を使って、確かめてみたいと思います。運動方程式の変数はvなので、変数分離すると、
<両辺をkで割る>
< − をかける>
両辺を時間tで積分します。
この数式の一般解を求めると、
ここで、時刻0のときの速度をv0とすると、式①より
となります。これで積分定数Cが決まりました。これを式①に代入すると、次のようになります。
ここで、式②の右辺の−mg/k+v0<0のとき、つまり初速度v0がmg/kよりも小さい場合には、
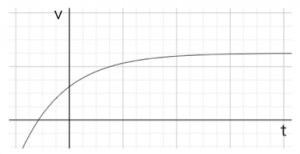
これをグラフにすると、
このよになります。時刻0のときの速度は、先ほどだしたので当たり前ですが、
また時間が無限大のときの速度、終端速度は
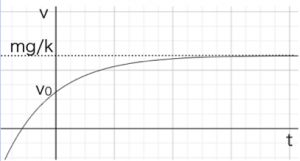
となります。これらをグラフに記入すると、
これが雨粒の落下の様子をしめします。雨粒は時刻0では初速度v0、そのときの傾きgで落下します。しかし空気抵抗の影響をうけると、徐々に速度が減っていき、最終的にはある一定の速度に落ち着きます。このとき、重力と空気抵抗がつりあっている状態です。
このような空気抵抗のある問題は入試問題では、終端速度を釣り合いの式から出すような問題以外は、あまり出題されることはないのですが、微積分を使うことにより、その落下の様子をイメージすることができて面白いですよね。
次回は、式②の右辺の−mg/k+v0>0のとき、つまり初速度v0がmg/kよりも大きい場合にはどのようになるのか考えてみましょう。これは小さな天体などが地球に衝突したときの様子になります。
雨に濡れない方法についてはこちらをご覧ください。
微積を使って物理を解く!その他のシリーズはこちらからどうぞ。
<力学>
等速度運動と微積
等加速度運動と微積
斜方投射と微積
空気抵抗のある落下運動
隕石の落下運動
微積で単振動を考えてみよう
単振動の数式とイメージを一致させよう!
単振動のエネルギーの表現方法
<電磁気分野>
<原子分野>
お問い合わせ・ご依頼について
科学の不思議やおもしろさをもっと身近に!自宅でできる楽しい科学実験や、そのコツをわかりやすくまとめています。いろいろ検索してみてください!
・科学のネタ帳の内容が本になりました。詳しくはこちら
・運営者の桑子研についてはこちら
・各種ご依頼(執筆・講演・実験教室・TV監修・出演など)はこちら
・記事の更新情報はXで配信中!
![]() 科学のネタチャンネルでは実験動画を配信中!
科学のネタチャンネルでは実験動画を配信中!